追尾機動 とは
追尾機動 の仕組み
ミサイルの有効範囲に関して考えるためにはまずミサイルの 追尾機動 自体を理解しておく必要があります。
本ブログではAIM-9Bを参考にしています。
Contents
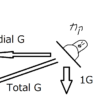
追尾機動中の距離と旋回率
中心が同じ円を描いて２機が飛んでいるときの関係は、計算から求めることができます。
[追尾機動中の距離]＝[自身の速度（フィート毎秒）]x[敵の速度（フィート毎秒）]xsin[2機の交差角]/32.2[自身のG]
[追尾機動中の旋回率]＝[敵の速度（フィート毎秒）]xsin[交差角]/[二機間の距離]
この式からGを掛けた状態＝半径が小さい状態 で交差角が同じなら二機間の距離が小さくなる事がわかると思います。しかし、上記の式は敵の動きや自分の飛行経路などを考慮していません。
この式で計算できるのは二次元平面状で、かつ二機の関係を自身のGと敵の速度だけで定義できる場合です。
実際にはこの式を元に計算した数値を参考にして、それぞれ別の状況で補正を入れて使うことになります。
上の式は戦闘中に使うものではなくあらかじめいくつかの数値を求めておいて使うものです。
代表的なものを自分の中で決めておいて近似します。
最大Gがかかる交差角
距離が詰まっていくと、だんだんかかるGが増えていきます。
cos[最大G時の交差角]＝[自身の速度]/(2x[敵の速度])
上記の式からどのタイミングで最大Gが掛かるかわかります。追尾機動での旋回中の交差角の変化からGの変化が予想できることと思います。
敵と自機が同速度のとき、交差角度60度で最大Gになります。